Sequential
Circuits
4.1
Introduction
Combination
circuits whose outputs are function of only the inputs were discussed. However,
in many digital designs there is a need for logic circuits whose outputs depend
not only on the present inputs, but also on the past values of the input and
output, of the circuit.
In other words,
the concept of time has to be introduced, and memory circuits are required to
store information about the past history of the circuit. Such circuits are
known as sequential logic circuits, because they follow a predetermined
sequence. There are numerous examples of sequential circuits, one of the most
widely met being the traffic light controller, which may be regarded as a black
box, as shown in Figure 4.1.
There are 3
outputs, labeled Red, Yellow and Green, to drive the 3 traffic lights, and a single
input, labeled clock. A light will be turned on if there is a 1 on its output
line. Fundamental to the design of sequential circuits is the concept of
internal states.
The simple
traffic light controller requires 4 states, labeled S0, S1,
S2 and S3, as shown in Figure 4.2. The lines drawn from 1
state to another show the transition between states. The input signal (or input
signal combinations) that gives rise to each transition is indicated above the
arrow. Each transition between states is initiated by a clock signal, clk, as
there are no other input signals in this simple example. Those outputs that are
turned on in a given state are shown either alongside, or inside the state
circles. For example, in state S1, Red and Yellow are on (1), while
Green is off (0).
4.2 Synchronous
and Asynchronous Sequential Circuits
There are 2
fundamentally different types of sequential circuit, namely synchronous and
asynchronous. In a asynchronous (or event driven) circuit there is no clock,
and transitions between states are initiated by changes in the appropriate
input signals. In a synchronous circuit, transitions between states are
initiated by a pulse from a single clock. It is normally assumed that any
changes in the input signals occur between clock pulses, so that the input
signals are stable when a clock pulse is applied. Synchronous circuits are easier
to design, and so this text will be restricted to them.
Figure
4.3 shows 2 typical clock signals. The first is a repetitive signal, derived
from an oscillator circuit, and has a constant frequency, f. At any instant in
time, its value is either 0 or VH where VH is the voltage
that corresponds to a 1 for the being used to implement the sequential design
(typically 5 volts). The period T of this clock signal is related to its
frequency by T = 1/f. The second clock signal although repetitive, does not have
a constant frequency. It is often referred to as a pulsed clock, the pulses
being generated in response to a change in one or more of the input signals. A
synchronous circuit is designed to change state either when the clock goes from
low to high, a positive edge transition, or when the clock goes from high to
low, a negative edge transition. The arrows in Figure 4.3 indicate the positive
transitions of the clock.
4.3 D-type
flip-flops
There
are 4 states, labeled S0 to S3, 2 state variables are
required, X and Y, say.
Each state variable is implemented with
a D-type flip-flop, so in this example 2 flip-flops are used. Both the inputs
and the outputs of the flip-flops are labeled with the suffixes X and Y,
respectively. The clock inputs are connected together, and are driven from a
single clock source, There are now 2 remaining problems, both involving
combinational logic, namely the interconnections required to the D inputs of
each flip-flop, and the logic required to generate the Red, Green and yellow
output signals from the state variables X and Y. The interconnections required
to the Dinputs of the flip-
flops are found by slightly modifying
the state table. This table for the traffic light controller is shown in Table
4.7. The states are now shown by their state variables; the assignment of each
variable combination to a given state is up to the designer but it is simplest,
at least initially, to follow the normal binary sequence. Note, however, that
the choice of state variables can alter the amount of hardware require to
implement the necessary combinational logic; other assignments may result in
less hardware.
This
equation shows that the next output, or state, of the flip-flop is just equal
to the present value of the D input. Thus the entries in Table 4.7 for the next
state are just those required for the D inputs, Dx and Dy.
Scanning
down the column labelled Y’ shows that there are only two 1 entries,
corresponding to the present states S1 (Y’.X) and S2 (Y,X’),
so that :
DY = Y’ .
X + Y .X’ = X+ Y
Similarly
for the X’ column there are also two 1 entries corresponding to states S0
and S2, and so :
DX = Y’ .
X + Y .X’ = X’
Figure
4.12 shows the two D-type flip-flops with the logic required to generates DX
and DY. Finally the logic required to generate the output signals
must be determined. Returning to the state diagram, it will be seen that the
following output signals are required.
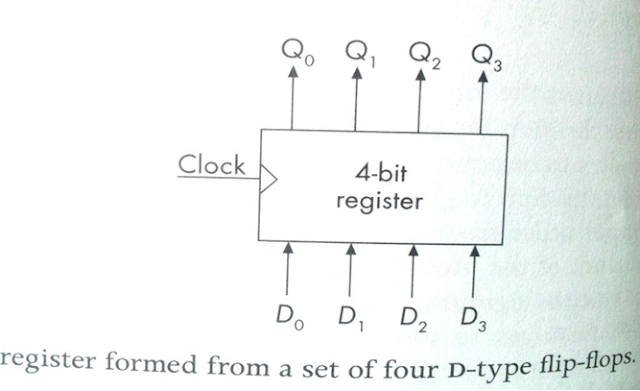
4.4 Register
A register is a device in which a
number of binary digits (bits) can be stored and retrieved, or read back. The
use of a D-type flip-flop to store a single bit of information. The data bit to
be stored in, or written to, the memory (0,1) is placed on the D input and a
clock pulse is then applied to the clock input. This results in the data bit
being stored in the flip-flop. Its value can be ascertained at any time from
the memory by reading the value of the Q output. A set of n of these D-type
flip-flops, fabricated as a single unit, can be used to store n bits of
information, and is known as a register. Frequently, n is a power of 2, usually
4, 8, 16, 32 or 64. Figure 4.22 is a schematic diagram of a single 4-bit
register.
The inputs are
labeled D0 to D3, and the outputs Q0 to Q3.
The pattern of bits stored in the register will be referred to as a (4-bit)
word. The 4 clock inputs to the individual flip-flops within the register are
connected to a common clock line. When a pulse is applied to this line the data
on the output lines are written into the memory, over-writing the previous word
stored.
4.5 Counter
Counters are a special class of finite
state machine. A counter follows a preset sequence and repeatedly outputs the
same pattern. The simplest counter is the binary-up counter in which the
counter is incremented by one each time a clock pulse occurs, until the maximum
count is reached. Figure 4.19 shows the state diagram for a modulo-8 counter.
By convention
the count begins at 0 and is then incremented by 1 on the next clock pulse
until the maximum of 7 occurs. When the next clock pulse occurs the counter is
reset to zero, and the sequence starts again. There are no inputs, apart from
the clock. Eight states require 3 state variables, X, Y and Z. Where possible
the state assignments are made so that the circuit outputs are just the state
variables, X, Y and Z. Thus, S0 = 000, S1 = 001 etc.
The design of a
synchronous counter proceeds in exactly the same way as discussed above for any
synchronous sequential circuit. For example, consider the design of a modulo-3
up/down synchronous counter. This counter has a single input labelled up/down,
in addition to the normal clock. If up/down = 1 the counter is to count up in
the normal way, following the sequence 0, 1, 2, 0, …, while if up/down = 0 it
is required to count down following the sequence 0, 1, 2, 0, … There are 3
states, so two state variables are required, X and Y. In normal operation the 4th
state, state 4, is never entered and so could be regarded as a ‘don’t care’
state. However, if state is ever entered (Eg : as the random state entered when
power is first switched on) then the next state should be one of the 3 states,
state 0 say, so that the count sequence is properly resumed.
In this example
it will be assumed that each of the state variables, X and Y, is stored in a JK
flip-flop, as shown in Figure 4.20. As before, the problem comes down to
designing the combinational logic required for the connections to the J and k inputs
of the 2 flip-flops, and the logic to generate the output signals. The logic is
determined by expanding the state table into a new modified table, called an
excitation table, Table 4.10 (b). Again the normal binary pattern has been
assumed for the state variables. The column labelled JK flip-flop controls is
filled in with the aid of the JK flip-flop state change table, table 4.6.
The decision on
whether to use D-type or JK flip-flops is really a matter of designer choice. A
JK flip-flop implementation is slightly more difficult to design, but will
often result in less hardware being required for the combinational logic, than
an equivalent design using D-type flip-flops.
Another type of
counter that is frequently used is the asynchronous or ripple counter. These
counters use JK flip-flops connected in the toggle mode, with J = K = 1.Figure
4.21 (a) shows a modulo-16 ripple counter. The pulses to be counted are applied
to the clock input of the first JK flip-flop. The output of this flip-flop, QA,
is applied to the clock input of the second flip-flop. Its output is applied in
turn to the clock input of the third flip-flop, and so on.
The first
flip-flop toggles, that is, changes state, on the rising edge of each of the
pulses to be counted. It effectively divides the pulse frequency by 2. The
second flip-flop toggles on every rising edge of QA, so effectively
dividing the input pulse frequency by 4. The outputs of the flip-flops are thus
a binary count of the input pulses, with QA being the least
significant digit, and QD the most significant digit. Clearly the
design can be extended to any number of stages to produce a modulo-N counter,
but with the limitation that N is a power of two. It is also possible to design
ripple counters where n is not a power of two, but their design is not
considered here. Note also that a modulo-N counter may also be used as a
divide-by-N frequency divider, dividing the input frequency by N, N2,
N4, etc. The name ‘ripple counter’ comes from the fact that changes
in the state of the counter ripple through the chain of flip-flops, with the
result that there is a propagation delay between the outputs of the flip-flops
changing. If this is important, then a synchronous counter must be used. In
such a counter, all the changes occur instantaneously coincident with the clock
pulse.
Written by,
Goh Hooi Kuan
B031210043










No comments:
Post a Comment